En estadística aplicada, uno de los métodos más usados para determinar la función de supervivencia es el estimador no paramétrico descrito en 1958 por el matemático Edward L. Kaplan y el estadístico Paul Meier. Sus aplicaciones prácticas son muy variadas y van mucho más allá de lo que uno entendería de entrada por ‘supervivencia’. Porque en medicina solemos usar el método de Kaplan-Meier, sí, para medir la fracción de pacientes que siguen con vida después de un tratamiento u otra intervención; pero puede usarse también para cualquier otro tipo de suceso de interés, además de la muerte: una enfermedad concreta, un acontecimiento adverso a la medicación, la aparición de intolerancia a la leche, la rotura de un empaste dental, etc. Y lo mismo cabe decir fuera de la medicina: un economista puede usarlo para medir el tiempo que permanece en paro un desempleado; un ingeniero, para medir el tiempo transcurrido hasta que falla un motor de combustión.
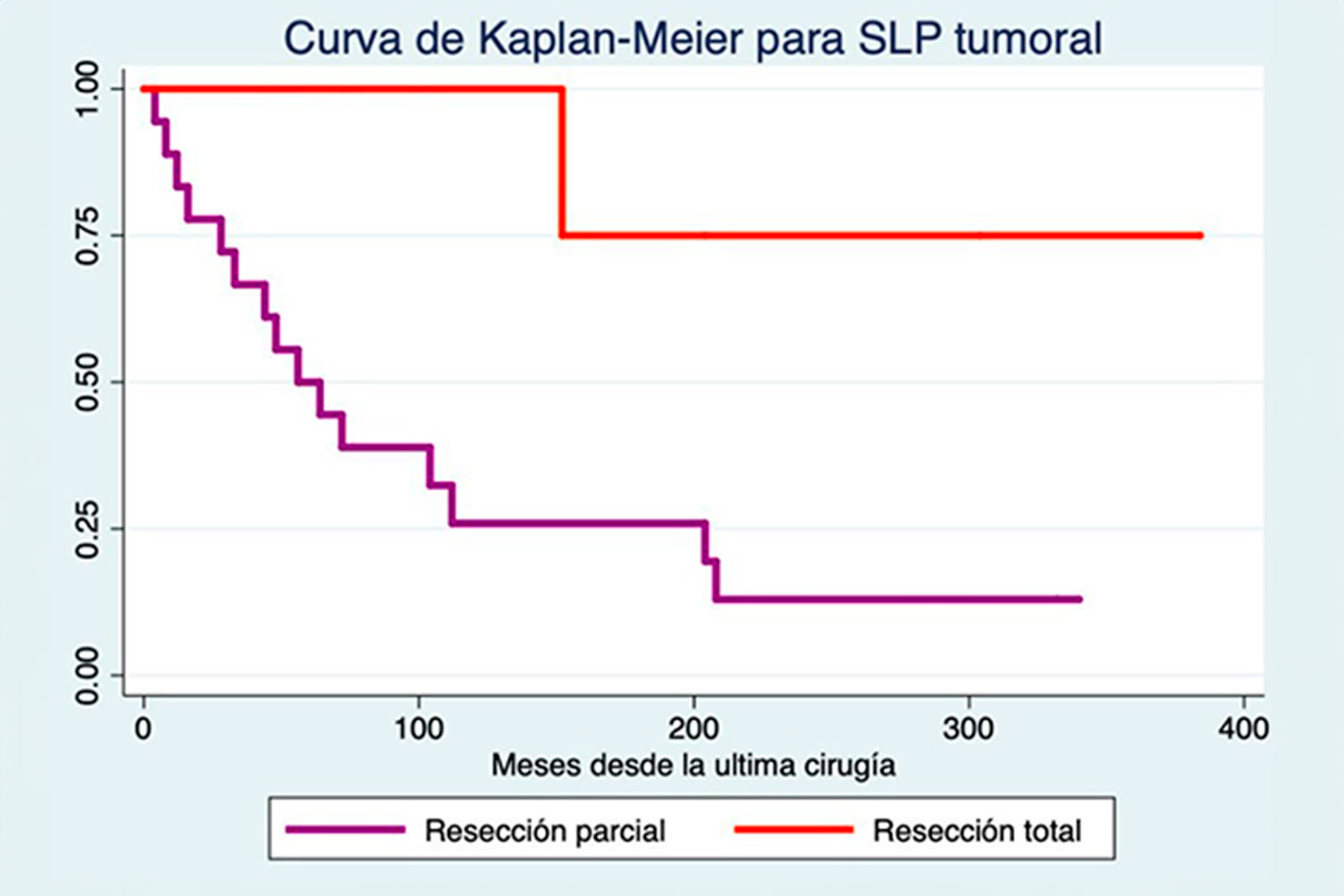
Para el análisis de la supervivencia, este estimador no paramétrico suele representarse gráficamente mediante lo que de modo habitual llamamos Kaplan-Meier curve en inglés y curva de Kaplan-Meier en español. Nombre este recogido en los diccionarios especializados, pero que nunca me ha terminado de convencer. Para empezar, porque normalmente no se trata de una sola curva, sino de al menos dos que se pretende comparar entre sí. Pero, sobre todo, porque nunca nunca nunca es una curva.
¿Han visto ustedes alguna vez una curva de Kaplan-Meier? Sí, ¿verdad? En el eje horizontal de abscisas (x), se representa el tiempo; en el eje vertical de ordenadas (y), la tasa de supervivencia (entendida, como acabo de explicar, en el sentido de tiempo transcurrido hasta la aparición de un suceso determinado, no necesariamente la muerte); y el trazado resultante tiene forma de línea quebrada, de escalera descendente con trazos rectos horizontales y verticales que van marcando los sucesivos escalones conforme va disminuyendo el número de integrantes de la población inicial que siguen sin presentar el suceso.
Y si no es una curva, sino una línea quebrada formada por segmentos rectos, ¿por qué la llamamos *curva de Kaplan-Meier*? Pues eso justamente me pregunto yo; y me pregunto también si no deberíamos empezar a llamarla gráfico de Kaplan-Meier. ♦
Off Fernando A. Navarro Offvia Noticias de diariomedico.... https://ift.tt/1cEqUIi


No hay comentarios:
Publicar un comentario