Cuando, referido a un sistema de microscopia, hablamos de aumento, nos referimos siempre a «aumento lineal (o unidimensional)» o, lo que es lo mismo, cuántas veces mayor que en la realidad es una línea vista a través del microscopio. Y resulta muy útil que sea así, porque, en relación con las mediciones cuantitativas, anatomopatólogos y microbiólogos usan los microscopios, básicamente, para medir segmentos lineales, como pueden ser el grosor de una membrana celular o el diámetro de una célula. Por lo que expresar la capacidad de aumento de un microscopio en aumentos lineales facilita mucho los cálculos: una línea de 300 nm de longitud vista a través de un microscopio de 10 000 aumentos, por ejemplo, medirá 10 000 veces más; esto es, 3 000 000 nm (o, lo que es lo mismo, 3 mm).
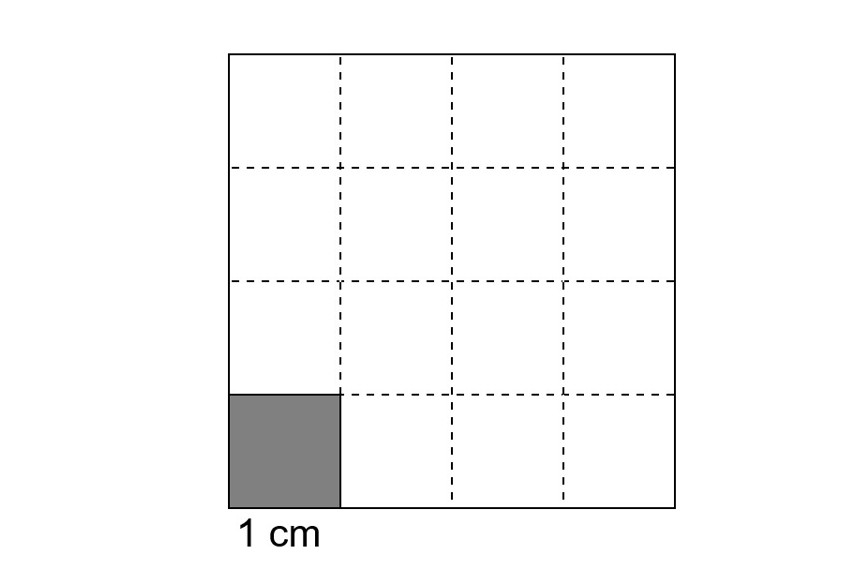
Los problemas comienzan cuando usamos un microscopio para valorar no medidas lineales (como una longitud, un diámetro o un grosor), sino medidas de superficie, como el área ocupada por una lesión maligna, el tamaño de una vacuola intracitoplásmica o la superficie de un núcleo celular. Porque en estos casos estamos observando las estructuras microscópicas con un «aumento superficial (o bidimensional)», pero seguimos expresando la capacidad de aumento del sistema óptico en aumentos lineales. Y las diferencias pueden ser considerables. Me serviré, para demostrarlo, de un ejemplo sumamente sencillo: una lupa de tan solo cuatro aumentos. En la figura siguiente tenemos, en sombreado, un cuadrado de 1 cm de lado (que ocupa, pues, una superficie de 1 cm2), y, en blanco, su imagen ampliada con una lupa de cuatro aumentos (lineales). Como puede apreciarse, cada lado del cuadrado ampliado ―que es una medida lineal― mide exactamente cuatro veces más que la del cuadrado original (4 × 1 cm = 4 cm). Pero la superficie del cuadrado ampliado ―que es una medida bidimensional― no es cuatro veces mayor que la del cuadrado original, sino 4 × 4 (es decir, 42) o, lo que es lo mismo, 16 veces mayor que la del cuadrado original (16 × 1 cm2 = 16 cm2), como puede comprobarse fácilmente contando el número de cuadraditos de bordes punteados (idénticos al cuadrado original) contenidos en el gran cuadrado blanco ampliado.
Es importante tener presente que este ejemplo se basaba en una mísera lupa de cuatro aumentos (lineales), y que la diferencia existente entre «aumento lineal» y «aumento superficial» crece exponencialmente cuanto mayor sea el aumento lineal de un microscopio. Si tenemos en cuenta que un microscopio electrónico puede llegar fácilmente a los 400 000 aumentos (lineales), el área ocupada por una mitocondria observada con un microscopio de tal potencia no será, como muchos erróneamente creen, 400 000 veces mayor, sino 400 0002 = 160 000 000 000; es decir, que las estructuras bidimensionales observadas con un microscopio de cuatrocientos mil aumentos son en realidad ¡ciento sesenta mil millones de veces mayores!
Y tampoco termina aquí la cosa. Porque, aunque acostumbrados a trabajar con cortes histológicos finísimos, los microscopistas acaban por suponer que todas las estructuras celulares son bidimensionales, en realidad son tridimensionales. Y un microscopio tridimensional nos ofrecería imágenes con «aumento espacial (o tridimensional)», cuya diferencia con el aumento lineal nominal será aún mayor. Retomando el caso de la lupa de cuatro aumentos (lineales), un cubo de 1 cm de lado sería no cuatro veces mayor, sino 4 × 4 × 4 (es decir, 43) o, lo que es lo mismo, 64 veces mayor. Y en el caso del microscopio de 400 000 aumentos lineales, una masa de células neoplásicas sería no 400 000 veces mayor, sino 400 0003 = 64 000 000 000 000 000; es decir, que una estructura tridimensional observada con un microscopio de cuatrocientos mil aumentos es en realidad ―agárrese el lector― ¡¡¡sesenta y cuatro mil billones ―con b― de veces mayor!!!
Fernando A. Navarro
Columna publicada originalmente en la revista Actas Dermosifiliográficas (2003)
via Noticias de diariomedico.... https://ift.tt/2TtMxy8


No hay comentarios:
Publicar un comentario